Numerik partieller Differentialgleichungen
Aktuelles
Am 8. Februar ist von 8:45-10:15 Uhr und von 12:30-14:00 Uhr Vorlesung. Die Übung findet von 10.30-12.00 Uhr in 00.74 statt.
Am 9. Februar entfällt dann die Vorlesung.
Die Vorlesung am 2. Februar 2017 entfällt. Am 2. Februar 2017 von 12:30 Uhr bis ca. 14 Uhr findet
im Hörsaal 3H (Geb. 23.21) die Studierendenvollversammlung des AStA für das
Wintersemester 2016/17 statt.
Begleitend zu dieser Vorlesung findet ein
Projektseminar statt.
Vorbesprechung am 19. Januar 2017 14:10 Uhr im Besprechungsraum 02.52 .
Personen
Umfang
4 SWS Vorlesung +
2 SWS Übungen
Zeit und Ort
Vorlesung: Mittwoch 8:30-10:15 Uhr in 2522.U1.34
und
Donnerstag 12:30-14:15 Uhr in 2522.U1.34
Übung: Mittwoch 12:30-14:30 Uhr in 2522.00.74
Inhalte
Numerische Behandlung elliptischer und parabolischer partieller Differentialgleichungen. Es werden finite Differenzen- und finite Elemente-Verfahren zur Ortsdiskretisierung vorgestellt, analysiert und an konkreten Anwendungsproblemen getestet. Zur Lösung parabolischer Differentialgleichungen wird diese Ortsdiskretisierung mit Verfahren zur Lösung gewöhnlicher Differentialgleichungen kombiniert.
Kreditpunkte
9 für die Vorlesung mit Übungen.
Die Kreditpunkte werden bei Bestehen der Prüfung vergeben.
Die aktive und erfolgreiche Mitarbeit in den
Übungen wird für die Zulassung zur Prüfung vorausgesetzt.
Prüfungen
Mündlich am 17.2. und am 2.3. Schreiben Sie mir eine e-mail mit ihrer Wunschzeit.
-
Freitag 17. Februar 2017
- 9:00 Uhr C. B.
- 9:30 Uhr A. B.
- 10:00 Uhr K. W
- 11:00 -12:30 Uhr E. S.
-
Donnerstag 2. März 2017
- 9:00 Uhr J. H.
- 9:30 Uhr C. G.
- 10:00 Uhr S. L.
- 10:30 Uhr J. D.
- 11:30 Uhr R. K.
- 12:00 Uhr K. P.
- 12:30 - 13:30 Uhr Mittagspause
- 14:00 Uhr K.K.
- 15:30 Uhr L.L.
-
Freitag 24. März 2017
- 12:30 Uhr J.H.
- 13:00 Uhr M.M.
- 13:30 Uhr N.S.
- 14:00 Uhr K.K.
-
Mittwoch 29. März 2017
Bei Bedarf gibt es weitere Termine.
Module:
Angewandte Mathematik, Numerik, Spezielle Themen der Numerik
Voraussetzungen:
Grundkenntnisse der Numerik wie sie zum Beispiel in der
Vorlesung Numerik I vermittelt werden
sowie Programmierkenntnisse in Matlab oder einer höheren
Programmiersprache.
Kenntnisse aus der Vorlesung Numerik II oder der Numerik gewöhnlicher
Differentialgleichungen werden nicht voraussgesetzt.
Literatur:
- Brenner, Susanne C. und Scott, Larkin Ridgway,
The mathematical theory of finite element methods.
3. ed., Springer, 2008. (elektronisch aus dem Uninetz)
- Braess, Dietrich, Finite Elemente - Theorie, schnelle Löser
und Anwendungen in der Elastizitätstheorie
4. überarb. und erw. Aufl., Springer, 2007. (elektronisch aus dem Uninetz)
Übungsblätter (pdf)
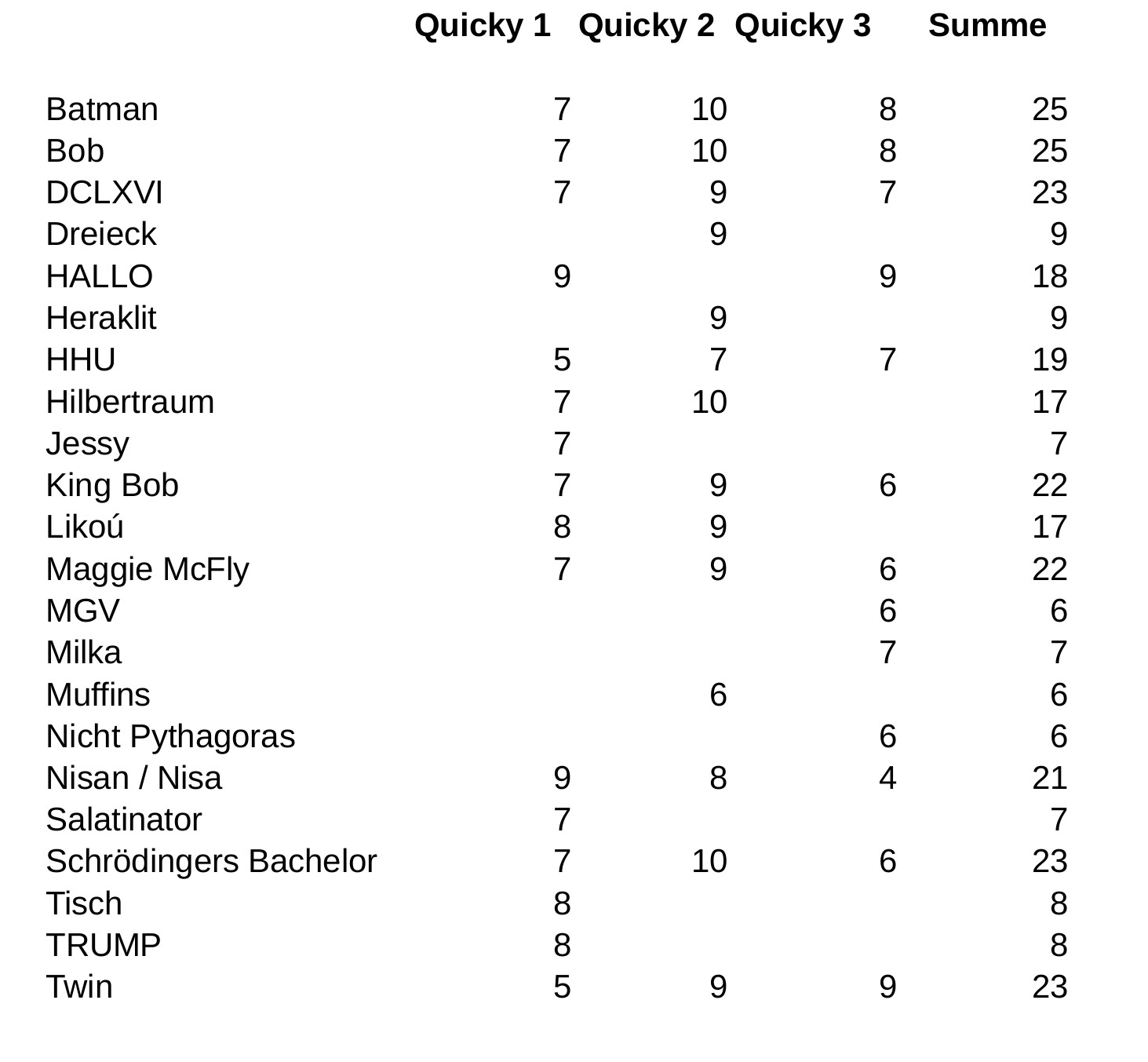
Quickys
Begleitmaterial
Matlabdateien
-
Zur Programmieraufgabe 12 fdtest.m .
-
Lagrange Basis der Ordnung 1 auf Dreiecken plotBasis.m .
-
Lösung zu Programmieraufgabe 12 a) fdO2.m .
-
Lösung zu Programmieraufgabe 12 b) fdO4.m .
-
Testskript zu Programmieraufgabe 12 TestAufg12.m .
-
Lösung zu Programmieraufgabe 16 Aufg16.m .
-
Lösung zu Programmieraufgaben 42 und 43 la42_43.m .
· Universitätsstraße 1
·
40225 Düsseldorf
Tel.: +49/(0)211/81-12189
· Fax: +49/(0)211/81-11829
· Impressum>
· Datenschutz last modified on:middot; last modified on: 18 July 2023 at 1:13pm.